Data d’elaboració: 31 de març de 2020
CONTEXT
L’estudi de les malalties infeccioses sovint es basa en models epidemiològics matemàtics que intenten emular la dinàmica de la malaltia i estimar els paràmetres relacionats amb ella, com ara la taxa de reproductibilitat, la taxa de mortalitat, etcètera.
La forma bàsica d’aquesta mena de simulacions són els models SIR basats en el cas que la població es pot classificar en tres grups compartimentats independents (persona susceptible, infectada i recuperada). El número i tipus de grups compartimentats es poden modificar per reflectir millor la dinàmica específica de la malaltia, com als models SEIR (persona susceptible, exposada, infectada i recuperada). Els models estudien com poden progressar els individus d’un grup compartimentat al següent.
Es poden diferenciar dues classes de models. Els deterministes es basen en equacions diferencials (sovint utilitzades per a poblacions grans), mentre que els models estocàstics es basen en processos de Markov (rellevants per a poblacions petites o amb gran variabilitat en els seus paràmetres). La Viquipèdia ofereix una descripció general per a conèixer una mica millor aquests models epidemiològics per grups compartimentats, i altres revisions ofereixen informació tècnica d’un nivell més avançat [1,2].
Els models que caracteritzen la COVID-19 generalment agreguen més grups compartimentats per cobrir aquells grups de població que s’infecten però que són asimptomàtics, els individus amb malaltia lleu que no necessiten hospitalització, aquells que necessiten hospitalització, aquells que necessiten cures crítiques i també aquells que moren. Els models que inclouen les categories de pacients hospitalitzats i/o pacients en cures crítiques permeten estimar les necessitats de llits d’hospital i UCI, que són clau en la planificació dels serveis sanitaris.
Aquest informe identifica i descriu breument els models matemàtics proposats que permeten estimar les necessitats de llits d’hospitalització i/o tractament a les unitats de cures intensives a causa de la COVID-19.
METODOLOGIA
Es van cercar estudis (inicialment el 20 de març, amb una actualització el 30 de març de 2020) en el repositori de preimpressions de publicacions científiques medRxiv (medrxiv.org) amb els termes ‘covid model’, i es va buscar a PubMed amb la següent sintaxi:
(((coronavirus[Title/Abstract]) OR covid[Title/Abstract])) AND ((((((decision modeling[MeSH Terms]) OR modelling[Title/Abstract]) OR model[Title/Abstract]) OR SIR[Title/Abstract]) OR microsimulation) OR markov)
Vam incloure models matemàtics quantitatius, definits com un “marc matemàtic que representa variables i les seves interrelacions per descriure fenòmens observats o predir esdeveniments futurs” [3]; que són sovint utilitzats per assistir en la presa de decisions en salut. Excloem d’aquesta revisió ràpida models estadístics utilitzats per estimar les associacions entre les variables mesurades o la seva distribució (per exemple, models de riscos proporcionals) o models utilitzats per a síntesis de dades (per exemple, model d’efectes fixos).
Es van identificar un total de 98 referències a Pubmed i 390 a medRxiv. Es van seleccionar sis publicacions [4-7], després de descartar referències d’estudis que no es basaven en un model matemàtic i models que no van considerar explícitament la necessitat d’hospitalització o UCI. Les publicacions seleccionades van ser preimpressions que encara no han estat avaluades per experts. Addicionalment, es van seleccionar quatre recursos en línia basats en models matemàtics que s’havien descrit en alguna de les publicacions excloses.
INFORMACIÓ RELLEVANT
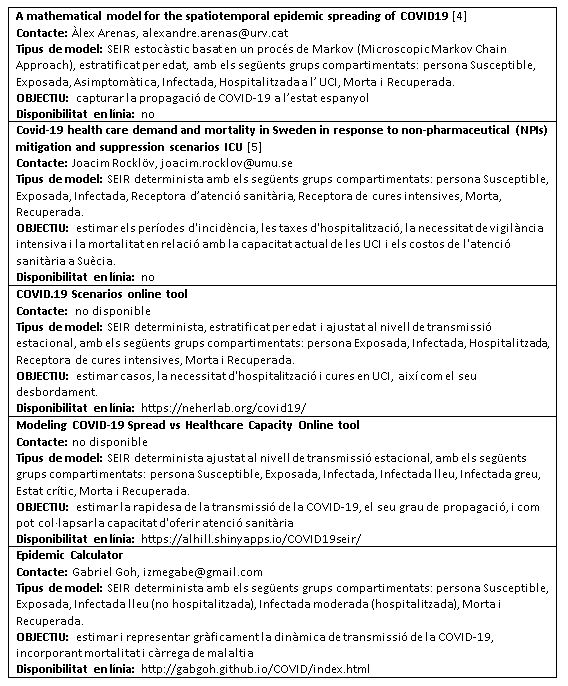
Dels 10 models valorats, cinc van incloure models SEIR que inclouen grups compartimentats específics per a hospitalització i/o atenció a UCI, i en conseqüència van permetre estimar les necessitats de llits d’hospital i/o UCI (descrits en la Taula 1). Dos d’ells s’han adaptat a recursos en línia, que permeten explorar diferents escenaris de necessitats relacionades amb la COVID-19.
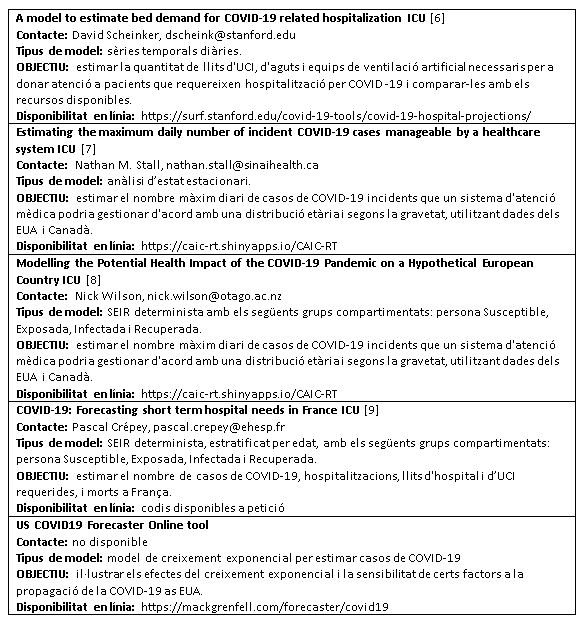
Els cinc models restants identificats no van incloure específicament els casos d’hospital i/o UCI en el model (Taula 2). En canvi, els van incloure com a paràmetres en un model general per a estimar la propagació de COVID-19, generalment com una fracció fixa de pacients amb COVID-19 que necessiten hospitalització o cures crítiques. Posteriorment, aquestes fraccions es van aplicar al nombre previst de casos de COVID-19 per obtenir les necessitats d’hospitalització o UCI. Aquests models s’han inclòs en aquest informe degut a la utilitat de les seves calculadores en línia (o codi disponible en un cas), que permeten explorar l’impacte de diferents fraccions d’hospitalització i/o UCI en el nombre esperat de llits necessaris.
TAULA 1. MODELS MATEMÀTICS PER ESTIMAR LA NECESSITAT DE RECURSOS A l’HOSPITAL I/O L’UCI:
TAULA 2. MODELS PRONÒSTIC PER A ESTIMAR LA NECESSITAT DE RECURSOS A l’HOSPITAL I/O L’UCI:
(aquests models no estimen explícitament les necessitats d’hospitalització, de vigilància intensiva o de ventilació, sinó que inclouen la fracció de pacients amb COVID-19 amb aquestes necessitats com a paràmetres al model.)
Referències
[1] Blackwood JC, Childs LM. An introduction to compartmental modeling for the budding infectious disease modeler. LETTERS IN BIOMATHEMATICS 2018, VOL. 5, NO. 1, 195–221
[2] HuppertA Katriel GMathematical modelling and prediction in infectious disease epidemiology. Clinical Microbiology and Infection; 19 (11), November 2013, 999-1005
[3] Eykhoff, P. (1974). System identification: Parameter and State Estimation. London: John Wiley & Sons.
[4] https://www.medrxiv.org/content/10.1101/2020.03.21.20040022v1
[5] https://www.medrxiv.org/content/10.1101/2020.03.20.20039594v1
[6] https://www.medrxiv.org/content/10.1101/2020.03.24.20042762v1
Aquesta informació ha estat redactada per investigadors del Centre Cochrane Iberoamericà per contribuir a sintetitzar i actualitzar els resultats de la recerca disponible en relació amb la pandèmia provocada pel coronavirus SARS-CoV-2. Cap altra institució o organisme queda compromès pel contingut d’aquesta informació.